What Are Room Modes

Room modes are caused by sound reflecting off of various room surfaces. There are three types of modes in a room: axial, tangential, and oblique. Modal activity occurs at frequencies which are directly related to the dimensions of the room.

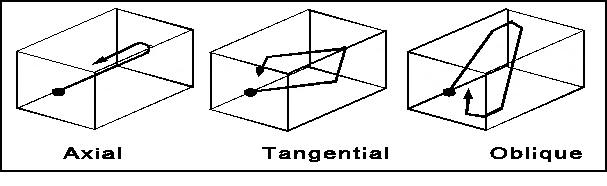
Axial modes are the strongest and many times, the only ones that are considered. Tangential and oblique room modes have less impact per mode but are also more prevalent. A combination of tangential and oblique modes can cause just as many issues as axial modes can.

Room modes can cause both peaks and nulls (dips) in frequency response. When two or more waves meet and are in phase with each other at a specific frequency, you will have a peak in response. When they meet and are out of phase with each other, they cancel and you end up with a dip or null in response.

Dealing with modes is accomplished by absorbing one of the boundaries to minimize the reflections off of it so there is nothing to combine or cancel. While corners are not a complete solution, they do offer the advantage of being at the end of 2 or even 3 of the room dimensions so there is a lot of benefit in that area. Sometimes there are modal issues which require treatment of the rear wall or even the ceiling over your head that treating corners would not solve.

Below is the formula for calculating all room modes, not just the axials.
F = c/2 * sqrt(p^2/L^2 + q^2/W^2 + r^2/H^2)

F= Frequency
c = speed of sound (1130 feet per second or 344 meters per second)
sqrt = Square Root
^2 = squared
L = Length of Room
W = Width of Room
H = Height of Room

p, q and r represent the mode we’re solving for. If you want to know the axial mode for the room length, p=1, q=0, r=0. If you want to know the 2nd axial, p=2, q=0, r=0. To find a tangential, use 1 in 2 of the variables. So, if you want the first tangential of the length and width, p=1, q=1, r=0.

Generally, as you go higher into the multiples (harmonics) of the modes, they become slightly less intense, but also occur at more places in the room.